Question

Help please!!!!!!!!!!!!!!

Answer 1

Part a)
`sin(U)=0.87`

Part b)
`cos(U)=0.50`

Part c)
`tan(U)=1.73`

Explanation:

step 1

we know that

In the right triangle UST

Applying the Pythagoras Theorem

Find the length side UT

`UT^(2)=(√(37))^(2)+(√(111))^(2)`

`UT^(2)=37+111`

`UT=√(148)\ units`

step 2

Find the sin(U)

we know that

The sine of angle U is the opposite side angle U divided by the hypotenuse

`sin(U)=(ST)/(UT)`

substitute the values

`sin(U)=(√(111))/(√(148))=0.87`

step 3

Find the cos(U)

we know that

The cosine of angle U is the adjacent side angle U divided by the hypotenuse

`cos(U)=(US)/(UT)`

substitute the values

`cos(U)=(√(37))/(√(148))=0.50`

step 4

Find the tan(U)

we know that

The tangent of angle U is the opposite side angle U divided by the adjacent side angle U

`tan(U)=(ST)/(US)`

substitute the values

`tan(U)=(√(111))/(√(37))=1.73`

Answer 2

Hello!

The answer is:

`Sin(u)=0.86\\Cos(u)=0.50\\Tan(u)=1.73`

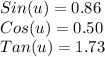
Why?

Since it's a right triangle, and we have the adjacent and opposite sides size (
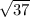`√(37)`), we can solve it using following the next steps:

Tan(u),

We can find the tangent using the following formula:

`tan(u)=(OppositeSide)/(AdjacentSide)= (√(111) )/(√(37))=(10.54)/(6.08)\\tan(u)=1.73`

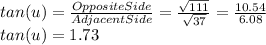
Sin(u),

To find the sin(u) we need first to find the hypotenuse of the triangle using the Pythagorean Theorem, so:

`c=\sqrt{a^(2)+b^(2)}`

Where:

`c=hypotenuse\\a=FirstTriangleSide\\b=SecondTriangleSide`

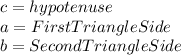
Substituting we have:

`hypotenuse=\sqrt{√(37)^(2)+√(111)^(2)}`

`hypotenuse=√(37+111)=√(148)=12.17`

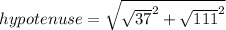
Then, we can calculate the sin(u) using the following formula:

`Sin(u)(OppositeSide)/(Hypotenuse)=(√(111) )/(12.17)=0.86`

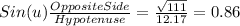
Finally, we can calculate the cos(u) by using the following formula:

Cos(u),

`cos(u)=(AdjacentSide)/(Hypotenuse)=(√(37) )/(12.17)=0.50`

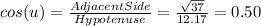
Hence,

We have that:

`Sin(u)=0.86\\Cos(u)=0.50\\Tan(u)=1.73`

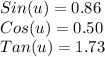
Have a nice day!