Question

What are the vertex and x-intercepts of the graph of the function below?

y = x2 - 4x - 21
A. Vertex: (2, -25); Intercepts: x = 3, -7
B. Vertex: (2, 17); Intercepts: x = -3, 7
C. Vertex: (2, 17); Intercepts: x = 3, -7
D. Vertex: (2, -25); Intercepts: x = -3, 7

Answer 1

I think is D.vertex(2_25);intercept:x=_3,7

Answer 2

Vertex: (2, -25); Intercepts: x = -3, 7

Explanation:

`y = x^2 - 4x - 21`

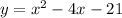
Lets find out the vertex and the x intercepts

To find out the vertex we use formula

`x=(-b)/(2a)`

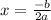
The value of a= 1, b=-4. Plug in the values

`x=(-(-4))/(2(1)=2)`

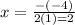
Substitute x=2 and find out y

`y = 2^2 - 4(2) - 21=-25`

So vertex (2,-25)

Now we find out x intercepts, replace y with 0 and solve for x

`0 = x^2 - 4x - 21`

we find out two factors whose product -21 and add upto -4

the factors are -7 and 3

`0 = (x-7)(x+3)`

`x-7=0, x=7`

`x+3=0, x=-3`

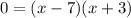
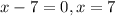
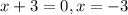
x intercepts are -3,7