Question

Before 1918, approximately 55% of the wolves in the New Mexico and Arizona region were male, and 45% were female. However, cattle ranchers in this area have made a determined effort to exterminate wolves. From 1918 to the present, approximately 70% of wolves in the region are male, and 30% are female. Biologists suspect that male wolves are more likely than females to return to an area where the population has been greatly reduced. (Round your answers to three decimal places.) (a) Before 1918, in a random sample of 9 wolves spotted in the region, what is the probability that 6 or more were male?

Answer 1

Step-by-step explanation: This answer is simple. Since 55% of the wolves were males subtract the amount of wolves by cattle and that's your answer

Answer 2

Explanation:

Given that before 1918, approximately 55% of the wolves in the New Mexico and Arizona region were male, and 45% were female.

a) Before 1918, in a random sample of 9 wolves spotted in the region, we have to find that the probability 6 or more were female

Let X be the no of males in the sample of 9 wolves

Each wolf is independent of the other to be male

Also there are only two outcomes

We have p = success for each outcome = 0.70

q =1-p =0.30

X is binomial with (9, 0.70)

the probability that 6 or more were male

=
`P(x\geq 6) \\=P(6)+P(7)+P(8)+P(9)+P(10)\\`

=
`\Sigma_6^9 9Cr (0.7)^r (0.3)^(9-r)`

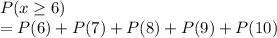
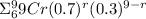
=0.7297