Question

Which of the following is NOT a valid strategy for solving the given equation?

a. To solved the equation cos²θ= sinθcosθ, first subtract sinθcosθ from both sides, then factor out the common factor of cosθ on the left side.b. To solve the equation cos²θ=sinθcosθ, ***FIRST DIVIDE**** both sides by cosθ.c. To solve sin2θ+2cosθsin2θ=0, first factor out the common factor of sin2θ on the left side.d. To solve the equation sinθ+cosθ=1, first square both sides of the equation.

Answer 1

The correct choice is B.

Explanation:

a. Given

`\cos^2(\theta)=\sin(\theta)\cos(\theta)`

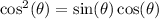
We can subtract
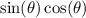`\sin(\theta)\cos(\theta)` from both sides to obtain;

`\cos^2(\theta)-\sin(\theta)\cos(\theta)=0`

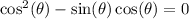
We can then factor
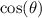`\cos(\theta)` to obtain;

`\cos(\theta)(\cos(\theta)-\sin(\theta))=0`

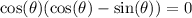
We can then proceed with our solution using the zero product principle.

b. Given
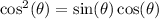`\cos^2(\theta)=\sin(\theta)\cos(\theta)`, it is not valid to divide both sides by
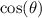`\cos(\theta)` because
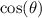`\cos(\theta)` could be equal to zero and division by zero in disguise will not result in the true solutions of the given equation.

c. To solve sin2θ+2cosθsin2θ=0, first factor out the common factor of sin2θ on the left side.

This is also a justifiable approach.

d. To solve the equation sinθ+cosθ=1, first square both sides of the equation.

Squaring both sides will help solve the equation with double angle properties easily.