Question

Kate packs snow into 5 identical jars. Each jar represents a different depth of snow. Kate then lets the snow in each jar completely melt. The table shows the height of the liquid in each jar as it relates to the original depth of snow in the jar.

Which statements are true about the relationship between the depth of the snow and the height of water in the jar after the snow is melted? Check all that apply.

The points on a graph representing the relationship lie on a line.
There is 0.4 inch of water to every 1 inch of snow.
A line through the points will pass through (0, 0).
The function relating snow depth to water depth is quadratic.
The data can be represented by f(x) = 0.2x.

Answer 1

A and C

Explanation:

Ok listen here. The guy from the other thing said ACE however thats so wrong that I can't explain how wrong that is. how is it wrong you might ask. Well if you can READ the question you know that you should select 2 options

second of all f(x)=0.2^x is saying that if x equals 2 then y is 0.2*0.2 which is 0.04 which is not the result.

I hope this helps more than whatever answer the other answer was. If not then you gotta figure it out yourself

Answer 2

A, C, E

Explanation:

From the table you can see that the water depth cahnges

`0.8-0.4=1.2-0.8=1.6-1.2=2.0-1.6=0.4\ in`

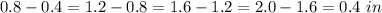
for every

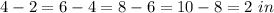`4-2=6-4=8-6=10-8=2\ in` of snow (option B is false).

This means that the function modelling this situation is linear function (option A is true and option D is false). Let the equation of this function be
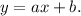`y=ax+b.` Then

`0.4=2a+b,\\ \\0.8=4a+b.`

Subtract these two equations:

`2a=0.8-0.4,\\ \\2a=0.4,\\ \\a=0.2.`

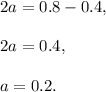
Hence,

`b=0.4-2\cdot 0.2=0.`

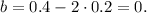
The equation of the straight line (the graph of linear function) is
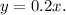`y=0.2x.` (option E is true) This line passes through the point (0,0), because its coordinates satisfy the equation (option C is true).