Answer:
4 hours
Explanation:
Let x minutes be the time needed for the powerful pomp to fill the pool. Then x+120 minutes is the time needed to the other pomp to fill the pool. The powerful pomp fills
 of the pool in a minute and the other pomp fills
of the pool in a minute and the other pomp fills
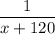 of the pool in a minute. Filling together, they fill
of the pool in a minute. Filling together, they fill
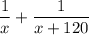 of the pool in a minute and
of the pool in a minute and

in 144 minutes.
Thus,
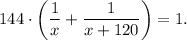
Solve this equation:
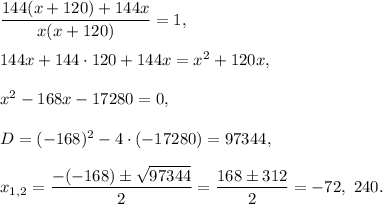
Hence, it is needed the powerful pomp 240 minutes = 4 hours to fill the pool.