Question

99 POINTS!! PLEAS HELP ASAP!!!!!

A rectangle ABCD is reduced by a scale factor of 0.5. AB = 16 and AC = 6.

(a) Calculate the length of each side of the reduced image.
(b) Draw the new image and label it .

Answer 1

Part a)
`A'B'=8\ units`,
`A'C'=3\ units`

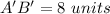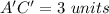
Part b) The graph of the reduced image in the attached figure

Explanation:

Let

z-----> the scale factor

x----> the length side of the reduced image

y----> the length side of the original image

so

`z=(x)/(y)`

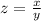
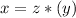`x=z*(y)` ----> equation to find the length side of the reduce image

we have

`z=0.5`

`AB=16\ units`

`AC=6\ units`

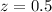
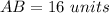
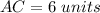
Part a) Calculate the length of each side of the reduced image

`A'B'=z*AB`

`A'B'=0.5*16=8\ units`

`A'C'=z*AC`

`A'C'=0.5*6=3\ units`

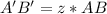
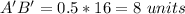
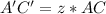
Part b) Draw the new image and label it

I assume that AB is the length of the original rectangle and AC is the width of the original rectangle

Using a graphing tool

see the attached figure