Question

A cylinder and a cone are shown below.​

Answer 1

For this case we have that the volume of a cylinder is given by:

`V_ {1} = \pi * r ^ 2 * h`

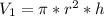
And the volume of a cone is given by:

`V_ {2} = \frac {1} {3} * \pi * r ^ 2 * h`

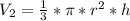
Where:

A: It's the radio

h: It's the height

In this case:

`V_ {1} = 2512 \ in ^ 3\\V_ {2} = 1256 \ in ^ 3`

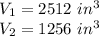
And the height is the same for both.

For the area of the bases to be equal, the volume of the cylinder must be 3 times the volume of the cone.

It is observed that:

`1256 \ in ^ 3 * 3 =\\3768 \ in ^ 3`

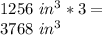
Then, it is not fulfilled.

Answer:

Option D