Answer:
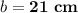
Explanation:
• To solve for a side using SOH CAH TOA, first check the angle whose measure is given.
In this case, we know ∠ C is 25°.
• Next we have to figure out the relationships between the given angle and two sides: one side whose length we know, and the other whose length we have to find.
In this case, the side opposite to ∠ C is known to be 10 cm, and the side adjacent to ∠ C is AC, whose length, b, we have to find.
• The trigonometric ratio that relates the adjacent and opposite sides of an angle is tan, where:
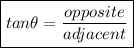 .
.
We can use this relationship to calculate the value of b:
⇒
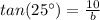
Solving for b:
⇒

⇒
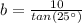
⇒
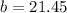
⇒
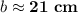 (rounded to the nearest whole number)
(rounded to the nearest whole number)