Answer:
The discontinuity of the given function f(x)=
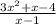 at x=1
at x=1
and zero of function f(x) is x=-1.33
Explanation:
Given function
f(x)=
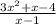
When we put x=1 then we get an indeterminate form
f(x)=
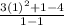
f(x)=
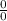 ( indeterminant form)
( indeterminant form)
Therefore , the function is discontinuous at x=1 .Hence, the discontinuity at x=1.
Now, we find zero of given function by putting f(x)=0
f(x)=0
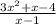 =0
=0
By splitting middle term of numerator we get
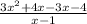 =0
=0
By factorization we get
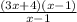 =0
=0
By simplification we get
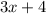 =0
=0
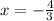
x=-1.33