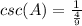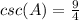Answer:
Part 1)
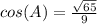
Part 2)
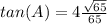
Part 3)
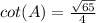
Part 4)
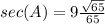
Part 5)
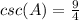
Explanation:
Let
A------> the angle
we have that
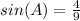
step 1
Find the cos(A)
we know that
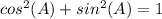
substitute the value of sin(A)
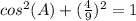
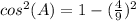
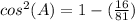
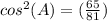
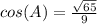
step 2
Find the tan(A)
we know that
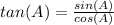
substitute the values
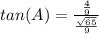
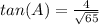
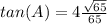
step 3
Find the cot(A)
we know that
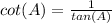
we have
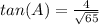
substitute
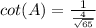
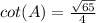
step 4
Find the sec(A)
we know that
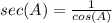
we have
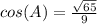
substitute
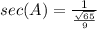
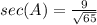
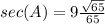
step 5
Find the csc(A)
we know that
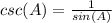
we have
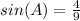
substitute the value