1.15 m/s to the left (3 sig. fig.).
Explanation
Momentum is conserved between the two balls if they are not in contact with any other object. In other words,
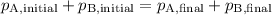
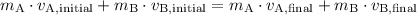 , where
, where
 stands for mass and
stands for mass and
 stands for velocity, which can take negative values.
stands for velocity, which can take negative values.
Let the velocity of objects moving to the right be positive.
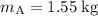 ,
,
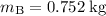 .
.
Before the two balls collide:
 ,
,
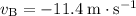 .
.
After the two balls collide:
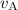 needs to be found,
needs to be found,
 .
.
Again,
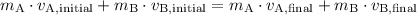 ,
,
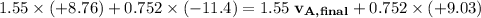 .
.
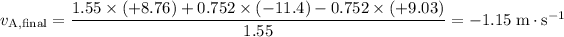 .
.
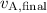 is negative? Don't panic. Recall that velocities to the right is considered positive. Accordingly, negative velocities are directed to the left.
is negative? Don't panic. Recall that velocities to the right is considered positive. Accordingly, negative velocities are directed to the left.
Hence, ball A will be travelling to the left at 1.15 m/s (3 sig. fig. as in the question) after the collision.