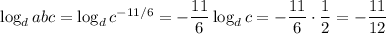We can expand the logarithm of a product as a sum of logarithms:

Then using the change of base formula, we can derive the relationship
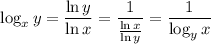
This immediately tells us that
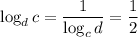
Notice that none of
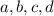 can be equal to 1. This is because
can be equal to 1. This is because
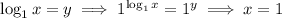
for any choice of
 . This means we can safely do the following without worrying about division by 0.
. This means we can safely do the following without worrying about division by 0.
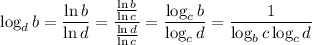
so that
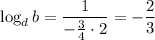
Similarly,

so that
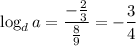
So we end up with
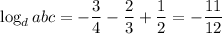
###
Another way to do this:
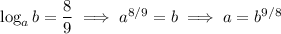
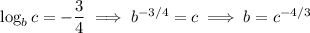
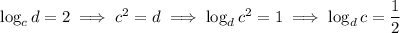
Then
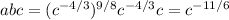
So we have