Question

Log6(-5r-2)=log6(r-4) Could someone help? I would be very grateful. And can you show the work?

Answer 1

`\log_6(-5r - 2) = \log_6(r-4)`

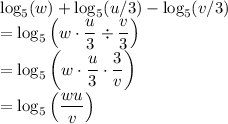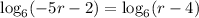
We can drop the logarithm base-6 because both sides have the same thing. In order for the two logaritms to be equal, the inside parts of the logarithm must be equal. Logarithm is a one-to-one function.

`\log_6(-5r - 2) = \log_6(r-4) \Rightarrow -5r - 2 = r- 4 \Rightarrow -6r = - 2 \Rightarrow r = 1/3`

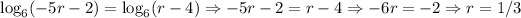
However, this solution does not work. If we try to use r = 1/3 into
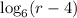`\log_6(r-4)` it yield
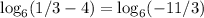`\log_6(1/3-4) = \log_6(-11/3)`. There is no real solution because logarithm cannot be negative.

For your new question,

`\displaystyle\log_5(w)+\log_5(u/3)-\log_5(v/3) \\= \log_5\left( w \cdot (u)/(3) / (v)/(3)\right) \\= \log_5\left( w \cdot (u)/(3) \cdot (3)/(v)\right) \\= \log_5\left( (wu)/(v)\right)`