Question

What is the measure of AC?​

Answer 1

AC=2AE ( because diagonal of rhombus bisect each others)

AE=8 cot 53°

AE=6

AC=2 x 6 = 12

Hence, The length of AC is 12

Answer 2

The length of AC is 12

Explanation:

we need to find measure of AC

Since, diagonal of rhombus bisect each others at 90°

AC = 2AE

In ΔAEB

Since,
`cot\theta=(base)/(perpendicular)`

`cot53=(AE)/(EB)`

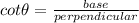
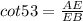
Since AE =EB = 8

`cot53=(AE)/(8)`

Multiply both the sides by 8,

AE = 8 cot 53°

AE = 8 * 0.75

AE = 6

so,

AC=2 x AE

AC=2 x 6

AC= 12

Hence, The length of AC is 12