Answer:
The shorter leg is
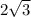 inches
inches
Step-by-step explanation:
The 30°-60°-90° is a special type of right-angled triangles
It has the following special side length:
The length of the side opposite to the 30° is
 the length of the hypotenuse
the length of the hypotenuse
The length of the side opposite to the 60° is
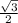 of the hypotenuse
of the hypotenuse
Now, we know that the lengths of the sides in a triangle are proportional to the angles
This means that the shortest side will be the one opposite to the smallest angles
In our case, the shortest side will be the one opposite to the 30° angle
We are given that the hypotenuse of the triangle is
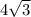 in
in
From the above:
Shorter leg = leg opposite to 30° =
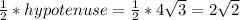 inches
inches
Hope this helps :)