Question

What is the slope of the function?

Answer 1

The function can be represented as y = -4x - 18.

Hence, the slope of the function is the coefficient of x, which is -4.

Answer 2

-4

Explanation:

With any 2 points of a function, we can calculate the slope dividing the "vertical change" by the "horizontal change".

That is, if our points are
`(x_1,y_1)` and
`(x_2,y_2)`, the slope (usually represented with the letter m) is
`m = (y_2-y_1)/(x_2-x_1)`

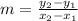
Let's choose any 2 points of the table, for example (1,-22) and (2,-26).

The slope is
`m = (-26-(-22))/(2-1) = (-4)/(1) = -4`

Let's see that we get the same slope if we choose other points, for example (-1,-14) and (-4,-2).

`m = (-2-(-14))/(-4-(-1)) = (12)/(-3) = -4`

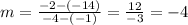
Therefore, the slope of the function is -4.