Question

A student factors 10x^2+3x-27 to the following. (2x-3)(5x+9)

which statement about (2x-3)(5x+9) is true?

A.The expression is equivalent, but it is completely factored
B.The expression is equivalent,but it is not completely factored
C.The expression is not equivalent, but it is completely factored
D.The expression is not equivalent,but it is not completely factored

Answer 1

Option A - The expression is equivalent, but it is completely factored

Explanation:

Given : A student factors
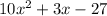`10x^2+3x-27` to the following (2x-3)(5x+9).

To find : Which statement is true about (2x-3)(5x+9) is true?

Solution :

First we are factoring the given quadratic equation,

`10x^2+3x-27=0`

Applying middle term split,

`10x^2+18x-15x-27=0`

`2x(5x+9)-3(5x+9)=0`

`(2x-3)(5x+9)=0`

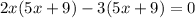
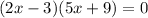
We have seen that the expression is completely factored and equivalent to given factor.

Therefore,Option A is correct.

The expression is equivalent, but it is completely factored.

Answer 2

A

Explanation:

The form (2x-3)(5x+9) is fully factored. To determine if it is equivalent, multiply the parenthesis out.

(2x-3)(5x+9) = 10x² - 15x + 18x - 27 = 10x² + 3x - 27

Yes this is equivalent.

The solution is A.