Question

A student in Greece discovers a pottery bowl that contains 48% of its original amount of C-14. Find the age of the pottery of bowl to the nearest year.

Answer 1

The correct answer is 4780

Answer 2

7340 years

Explanation:

A student in Greece discovers a pottery bowl that contains 48% of the original C-14.

Decay of C - 14 is represented by the expression given

N =
`N_(0)e^(-kt)`

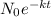
where,
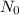`N_(0)` = initial quantity of C-14 = 100% = 1

N = quantity of C-14 after t years = 48% = 0.48

k = 0.0001

and t = time in years.

We have to find the age of the bowl.

0.48 =
`1(e)^((-0.001)(t))`

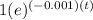
By taking natural logarithm

ln ( 0.48 ) = ln
`e^((-0.0001)(t))`

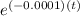
-0.73397 = -0.0001t [ since ln e = 1 ]

t =
`(0.73397)/(0.0001)`

t = 7340 years

Age of the pottery of bowl is 7340 years.