Question

The figure is a square. Its diagonals meet to form four right angles. What is the approximate value of x?

A. 2.8 units
B. 3.3 units
C. 4.0 units
D. 5.7 units

Answer 1

Hello!

The answer is: D. 5.7 units.

Why?

Since the diagonals meet to form four right triangles, we can use the following the Pythagorean Theorem.

We can see that the diagonals are equal, also, the other two sides of the triangle are also equal(x), it means that the other two angles are also equal to 45°.

Remember, the sum of the internal angles of a triangle are also equal to 180°.

We can use the following equation:

`sin(\alpha)=(OppositeSide)/(Hypotenuse)`

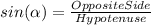
Where:

`\alpha=45\\OppositeSide=X\\Hypotenuse=8Units`

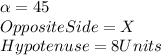
So, by substituting we have:

`sin(45)=(x)/(8Units)\\\\x=sin(45)*8Units=0.71*8=5.68Units`

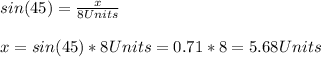
And,

5.68units rounded to the nearest tenth are equal to 5.7units

Hence, the correct option is D. 5.7 units.

Answer 2

The correct answer is option D. 5.7 units

Explanation:

It is given a square, Its diagonals meet to form four right angles

To find the value of x

From the figure we can see that the triangle with sides x, x, 8 have angles 45°,45° and 90°

If the angles are 45°,45° and 90° then sides are in the ratio 1 : 1 : √2

Here x : x : 8 = 1 : 1 : √2

Therefore x = 8√2 = 8/1.414 = 5.6577 ≈ 5.7 units

Therefore the correct answer is option D 5.7 units