Question

Alejandro reduced triangle A proportionally.

He made each side 1/2 as long.

Use the drop-down menus to complete the statements below.

Answer 1

Each side of triangle A changed by a factor of 1/2.

The unknown side length in triangle B has a measure of 7.5.

Explanation:

He made each side 1/2 as long so it changed by a factor of 1/2. 1/2 times 15 is 7.5.

Answer 2

(1) Each side of triangle A is changed by a factor of 1/2.

(2) The unknown side length in triangle B has a measure of 7.5 units.

Explanation:

It is given that Alejandro reduced triangle A proportionally.

It means triangle A and B are similar and their corresponding sides are proportional.

`\text{Scale factor}=\frac{\text{Side length of image}}{\text{Corresponding side length of primage}}`

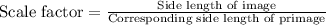
From the given figure it is clear that the side of length 12 units is reduce to 6 units.

`\text{Scale factor}=(6)/(12)`

`\text{Scale factor}=(1)/(2)`

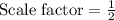
Each side of triangle A is changed by a factor of 1/2.

Let the unknown side of triangle B be x.

`(x)/(15)=(1)/(2)`

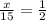
On cross multiplication we get

`2x=15`

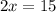
Divide both sides by 2.

`x=7.5`

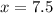
Therefore, the unknown side length in triangle B has a measure of 7.5 units.