Answer:
20)
![\displaystyle [4, 1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7e8apf0bbsuu8m60m9p661nwaf93jmnic7.png)
19)
![\displaystyle [-5, 1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jlt3puw2x8zj6ew73dfl5sapdi0wqk21h2.png)
18)
![\displaystyle [3, 2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4j0bevowpbg13alesvxqifmcpigpbttdmw.png)
17)
![\displaystyle [-2, 1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/imm2it5mrbko6mifonxb8tpe0wjf37iwk8.png)
16)
![\displaystyle [7, 6]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8v26mbpk0cg96ni3enpjqtk9iljs4z45s2.png)
15)
![\displaystyle [-3, 2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8f9g18cdwbbj32o4xiw7uwe4bgtb9yqpaj.png)
14)
![\displaystyle [-3, -2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ncemgoqqtxg9ftyyy3k5rl99brlyginm8e.png)
13)
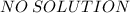
12)
![\displaystyle [-4, -1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6s5bik4sfu23w2bj66kdmve219i97zgbya.png)
11)
![\displaystyle [7, -2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wczw7cfplxidcm9djzbrqe1n9rfgmz6hii.png)
Explanation:
20) {−2x - y = −9
{5x - 2y = 18
⅖[5x - 2y = 18]
{−2x - y = −9
{2x - ⅘y = 7⅕ >> New Equation
__________
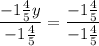
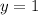 [Plug this back into both equations above to get the x-coordinate of 4];
[Plug this back into both equations above to get the x-coordinate of 4];
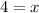
_______________________________________________
19) {−5x - 8y = 17
{2x - 7y = −17
−⅞[−5x - 8y = 17]
{4⅜x + 7y = −14⅞ >> New Equation
{2x - 7y = −17
_____________
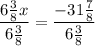
 [Plug this back into both equations above to get the y-coordinate of 1];
[Plug this back into both equations above to get the y-coordinate of 1];
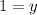
_______________________________________________
18) {−2x + 6y = 6
{−7x + 8y = −5
−¾[−7x + 8y = −5]
{−2x + 6y = 6
{5¼x - 6y = 3¾ >> New Equation
____________
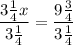
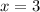 [Plug this back into both equations above to get the y-coordinate of 2];
[Plug this back into both equations above to get the y-coordinate of 2];
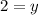
_______________________________________________
17) {−3x - 4y = 2
{3x + 3y = −3
__________
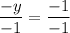
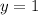 [Plug this back into both equations above to get the x-coordinate of −2];
[Plug this back into both equations above to get the x-coordinate of −2];
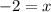
_______________________________________________
16) {2x + y = 20
{6x - 5y = 12
−⅓[6x - 5y = 12]
{2x + y = 20
{−2x + 1⅔y = −4 >> New Equation
____________
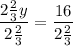
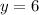 [Plug this back into both equations above to get the x-coordinate of 7];
[Plug this back into both equations above to get the x-coordinate of 7];
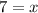
_______________________________________________
15) {6x + 6y = −6
{5x + y = −13
−⅚[6x + 6y = −6]
{−5x - 5y = 5 >> New Equation
{5x + y = −13
_________
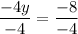
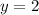 [Plug this back into both equations above to get the x-coordinate of −3];
[Plug this back into both equations above to get the x-coordinate of −3];
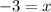
_______________________________________________
14) {−3x + 3y = 3
{−5x + y = 13
−⅓[−3x + 3y = 3]
{x - y = −1 >> New Equation
{−5x + y = 13
_________
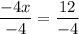
 [Plug this back into both equations above to get the y-coordinate of −2];
[Plug this back into both equations above to get the y-coordinate of −2];
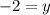
_______________________________________________
13) {−3x + 3y = 4
{−x + y = 3
−⅓[−3x + 3y = 4]
{x - y = −1⅓ >> New Equation
{−x + y = 3
________
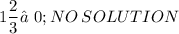
_______________________________________________
12) {−3x - 8y = 20
{−5x + y = 19
⅛[−3x - 8y = 20]
{−⅜x - y = 2½ >> New Equation
{−5x + y = 19
__________
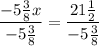
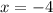 [Plug this back into both equations above to get the y-coordinate of −1];
[Plug this back into both equations above to get the y-coordinate of −1];
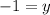
_______________________________________________
11) {x + 3y = 1
{−3x - 3y = −15
___________
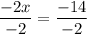
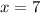 [Plug this back into both equations above to get the y-coordinate of −2];
[Plug this back into both equations above to get the y-coordinate of −2];
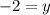
I am delighted to assist you anytime my friend!