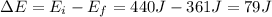Question

A spring has a force constant of 40,000 n/m. It is resting horizontally on a 20 m tall roof top and fires a 2 kg mass to the ground below. The mass hits the ground a 21 m/sec. How far was the spring compressed? (no energy was lost)

In the previous problem, if the mass hits the ground at 19 m/sec, how much energy was lost due to air resistance?

Answer 1

1) 4.9 cm

The initial mechanical energy of the spring+mass system is sum of gravitational potential energy and elastic potential energy of the spring:

`E=mgh+(1)/(2)kx^2`

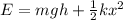
where:

m = 2 kg is the mass

g = 9.8 m/s^2

h = 20 m is the height of the roof top

k = 40,000 N/m is the spring constant

x is the compression of the spring

When the mass hits the ground, its mechanical energy is just kinetic energy:

`E=(1)/(2)mv^2`

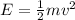
where v = 21 m/s is the speed. Since energy is conserved, we can equalize the two expressions, and solving for x we find the compression of the spring:

`mgh+(1)/(2)kx^2=(1)/(2)mv^2\\x = \sqrt{(mv^2-2mgh)/(k)}=\sqrt{((2 kg)(21 m/s)^2-2(2 kg)(9.8 m/s^2)(20 m))/(40000 N/m)}=0.049 m = 4.9 cm`

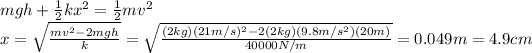
2) 79 J

The initial mechanical energy of the spring-mass system is

`E_i=mgh+(1)/(2)kx^2=(2 kg)(9.8 m/s^2)(20 m)+(1)/(2)(40,000 N/m)(0.049 m)^2=440 J`

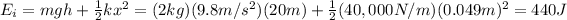
While the final mechanical energy of the mass is

`E_f = (1)/(2)mv^2 = (1)/(2)(2 kg)(19 m/s)^2=361 J`

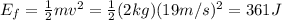
So, the energy lost due to air resistance is

`\Delta E= E_i - E_f = 440 J-361 J=79 J`