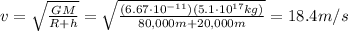Question

Suppose that the Millennium Falcon orbits the Death Star 20,000m above the Star’s surface. Calculate the circular orbit velocity in m/s

Answer 1

18.4 m/s

Step-by-step explanation:

The gravitational force between the Death Star and the Millenium Falcon is equal to the centripetal force that keeps the Millenium Falcon in circular orbit:

`G(Mm)/((R+h)^2)=m(v^2)/(R+h)`

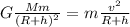
where

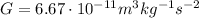`G=6.67\cdot 10^(-11) m^3 kg^(-1) s^(-2)` is the gravitational constant

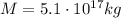`M=5.1\cdot 10^(17) kg` is the mass of the planet

`m=1.36\cdot 10^6 kg` is the mass of the Millennium Falcon

`v` is the orbital velocity of the Millennium Falcon

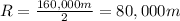`R=(160,000 m)/(2)=80,000 m` is the radius of the Death Star

`h=20,000 m` is the altitude of the Millennium Falcon above the planet's surface

Solving the equation for v, we find the orbital velocity:

`v=\sqrt{(GM)/(R+h)}=\sqrt{((6.67\cdot 10^(-11))(5.1\cdot 10^(17) kg))/(80,000 m+20,000 m)}=18.4 m/s`