Question

The planet Jupiter is about 300 times as massive as Earth, yet on its surface you would weigh only about 3 times as much. This is because

a. your mass is 100 times less on Jupiter
b. Jupiter is significantly farther from the sun
c. Jupiter's radius is 10 times the Earth's radius
d. you are 100 times more weightless there n
e. one of these

Answer 1

c- Jupiter's radius 10 times the Earth's radius

Step-by-step explanation:

Answer 2

c. Jupiter's radius is 10 times the Earth's radius

Step-by-step explanation:

The weight of a person on the surface of a planet is equal to the gravitational pull exerted by the planet on the person:

`F=G(mM)/(R^2)`

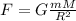
where

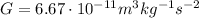`G=6.67\cdot 10^(-11) m^3 kg^(-1) s^(-2)` is the gravitational constant

M is the mass of the planet

m is the mass of the person

R is the radius of the planet

The weight of a person on Earth is given by:

`F_E=G(mM_E)/(R_E^2)`

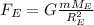
where
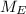`M_E` is the mass of the Earth and
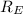`R_E` is the Earth's radius.

We know that Jupiter's mass is 300 times the Earth's mass:

`M_J = 300 M_E`

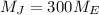
while Jupiter's radius is 10 times the Earth's radius:

`R_J = 10 R_E`

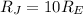
So, the weight of the person on Jupiter is

`F_J=G(mM_J)/(R_J^2)=G(m(300 M_E))/((10 R_E)^2)=G (300 mM_E)/(100 R_E^2)=3 G(mM_E)/(R_E^2)=3 F_E`

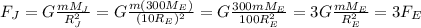
So, the weight would be only 3 times as much.