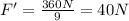Answer:
40 N
Step-by-step explanation:
The gravitational force between the asteroid and the spaceship is given by:
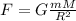
where
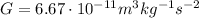 is the gravitational constant
is the gravitational constant
 is the mass of the asteroid
is the mass of the asteroid
 is the mass of the spaceship
is the mass of the spaceship
 is the distance between the asteroid and the spaceship
is the distance between the asteroid and the spaceship
The initial force is equal to:
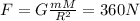
Later, the spaceship moves to a position 3 times as far from the center of the asteroid, so R' = 3R. Therefore, the new force will be
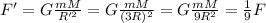
so, the force is decreased by a factor 9. Since the initial force was F=360 N, the new force will be