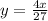For this case, we must simplify the following equation:
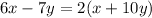
We apply distributive property to the terms of the parenthesis on the right side of the equation:
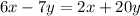
We subtract "2x" on both sides of the equation:
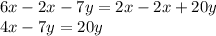
We add "7y" to both sides of the equation:
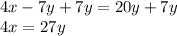
We clear one of the variables:
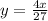
Answer: