Answer:
de Broglie wavelength of an electron with speed 0.78 c taking relativistic effects into account is given as:
λ = 1.943 * 10^(-12) m
Step-by-step explanation:
Given:
v = 0.78 c
we know:
c = speed of light = 3 * 10^8 m/s
mass of electron = m = 9.1 × 10-31 kg
de Broglie wavelength:
In 1924 a French physicist Louis de Broglie assumed that for particles the same relations are valid as for the photon:
(Dual-nature of a particle)
Let the wavelength be = λ
According to de Broglie:
λ = h/p = h/mv
where h is planck's constant = 6.626176 x 10^-34 Js
and p is momentum.
Taking relativistic effects into account, we know that the momentum of the particle changes by a factor 'γ'.
At low speed, γ is almost 1. However, at very high velocity (comparable to light), it has a great effect on momentum.
γ =
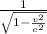
γ = 1.6
Now at 0.78 c, considering relativistic effects, we know:
λ = h/γp = h/γ*mv
= (6.62 x 10^(-34))/(1.6*0.78*3*10^(8)*9.1 × 10-31
λ = 1.943 * 10^(-12) m