Answer:
The measure of angle A is 53.13°.
Explanation:
Given,
ABC is a triangle,
In which m∠CBA = 90°, AB = 3 cm, BC = 4 cm and CA = 5 cm,
By the law of sine,
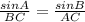
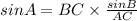 ( By cross multiplication )
( By cross multiplication )
By substituting the values,

 ( sin 90° = 1 )
( sin 90° = 1 )
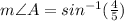
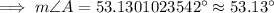
Hence, the measure of angle A is 53.13°.