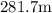Answer:
281.7m
Step-by-step explanation:
Given: A lifeboat is 55m directly below a rescue plane, constant vertical acceleration of 6.91
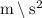 , horizontal speed of plane is
, horizontal speed of plane is
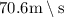
To Find: how far is the package from the lifeboat when it hits the waves
Solution: Verticle distance to cover=
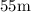
The emergency kit descends with acceleration of
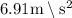
Using second equation of motion
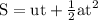
initial speed of emergency kit
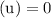
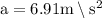
putting in equation
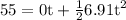
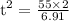
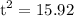
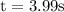
time taken by kit to hit the wave
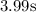
distace of kit from lifeboat=horizontal distance travelled by emergency kit
horizontal velocity of kit will be same as that of plane as kit is thrown from plane
horizontal distance travelled by emergency kit
using equation of motion
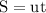
here
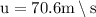
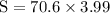
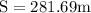 ≅
≅
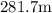
The distance of emergency kit from lifeboat is