Question

Gauss-Jordan Elimination

Answer 1

(Correct answer choices in boldface)

The total of the three payments comes out to $29000, so

`x+y+z=29000`

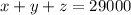
"Two times the first installment is $1000 more than the sum of the third installment and three times the second installment" translates to

`2x=1000+z+3y\implies2x-3y-z=1000`

The second and third installments have a 15% interest rate, but there's no interest on the first installment. The total interest owed is $2100, so

`0.15y+0.15z=2100`

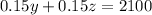
In augmented matrix form, this system is equivalent to

`\begin{bmatrix}1&1&1&29000\\2&-3&-1&1000\\0&0.15&0.15&2100\end{bmatrix}`

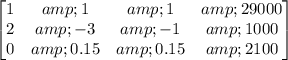
### Row 2, column 1 ### (not row 1, column 1)

The third equation is equivalent to

`\frac1{0.15}(0.15y+0.15z)=(2100)/(0.15)\iff y+z=14000`

so the third row in the matrix could adjusted to get

`\begin{bmatrix}1&1&1&29000\\2&-3&-1&1000\\0&1&1&14000\end{bmatrix}`

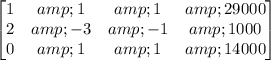
Also, adding the first row to the second gives

`\begin{bmatrix}1&1&1&29000\\3&-2&0&30000\\0&1&1&14000\end{bmatrix}`

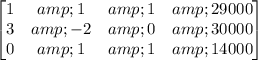
### Row 3, column 2 ### (not row 1, column 2)

Subtracting row 3 from row 1 gives

`\begin{bmatrix}1&0&0&15000\\3&-2&0&30000\\0&1&1&14000\end{bmatrix}`

Subtracting 3 times row 1 from row 2 gives

`\begin{bmatrix}1&0&0&15000\\0&-2&0&-15000\\0&1&1&14000\end{bmatrix}`

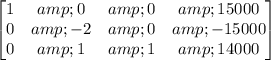
and multiplying row 2 by -1/2 gives

`\begin{bmatrix}1&0&0&15000\\0&1&0&7500\\0&1&1&14000\end{bmatrix}`

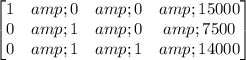
Finally, subtracting row 2 from row 3 gives

`\begin{bmatrix}1&0&0&15000\\0&1&0&7500\\0&0&1&6500\end{bmatrix}`

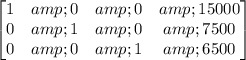
### Row 2, column 3 ### (not row 3, column 2)