Question

What is the solution set of the quadratic inequality 4(x+2)^2<_ 0

Answer 1

The solution set of the quadratic inequality 4(x+2)^2 ≤ 0 is x ≤ -2.

Step-by-step explanation:

The solution set of the quadratic inequality 4(x+2)^2 ≤ 0 can be found by completing the square. First, divide both sides of the inequality by 4 to obtain (x+2)^2 ≤ 0. Next, take the square root of both sides to eliminate the squared term. Since the square root of a number can only be positive or zero, we have x+2 ≤ 0. Finally, solve for x by subtracting 2 from both sides, resulting in x ≤ -2.

Answer 2

The solution of the given quadratic inequality is:

`x=-2`

Step-by-step explanation:

Solution of a inequality is the set of all the possible x value which satisfy the inequality i.e. it is the collection of all the possible value which makes the inequality true.

We know that the square of any quantity is always greater than or equal to zero.

i.e.

`(x+2)^2\geq 0`

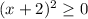
also,

`4(x+2)^2\geq 0`

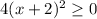
But we are given a inequality as:

`4(x+2)^2\leq 0`

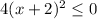
Hence, from (1) and (2) we get:

`4(x+2)^2=0`

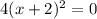
i.e.

`x=-2`

Hence, the solution is:

x= -2