Answer:
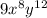
Explanation:
The expression is:
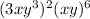
we use the following rule to simplify the expression:
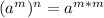
that is, we multiply the exponent inside the parentheses by the exponent outside the parentheses (also using
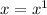 ):
):
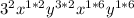
and we simplify the exponents and substitute
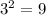 :
:
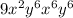
We have not finished simplifying yet, since we have that x and y are repeated we must use the following law of exponents:
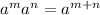
We add the exponents that each variable has.
thus, the expression becomes:
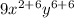
and we simplify the exponents:
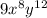
which is the fourth option