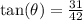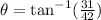QUESTION 1
The hypotenuse of the right triangle is
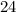 units
units
The side adjacent to the given angle is 21 units.
According to the Pythagoras' Theorem,
The length of the hypotenuse square is equal to the sum of the squares of the two shorter legs.
Let the second shorter side(opposite side) be
 units.
units.
Then;
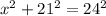
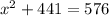


Take positive square root
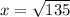
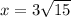
Recall the mnemonics: SOH CAH TOA
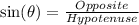
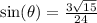
Simplify:
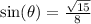
b) The co-secant ratio is the reciprocal sine ratio.
This implies that;



Rationalize the denominator;
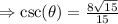
c) The cosine ratio is
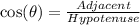
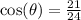
Simplify;

d) The secant ratio is the reciprocal of the cosine ratio;
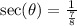

e) Recall and use the mnemonics TOA
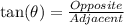
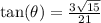
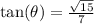
f) The co-tangent ratio is the reciprocal of the tangent

Rationalize the denominator;
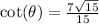
QUESTION 2
It was given that;
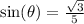
This means that
 units and
units and
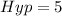 units.
units.
We apply the Pythagoras Theorem, to obtain;

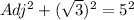

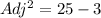
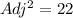

a) The co-secant ratio is the reciprocal sine ratio.
This implies that;



Rationalize the denominator;
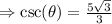
b) The cosine ratio is
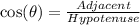
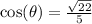
c) The secant ratio is the reciprocal of the cosine ratio;
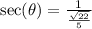
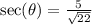
Rationalize the denominator;

d) Recall and use the mnemonics TOA
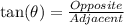
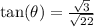
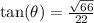
e) The co-tangent ratio is the reciprocal of the tangent

Rationalize the denominator;

QUESTION 3
We use the tangent ratio to find the opposite side.
i)
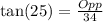
This implies that;
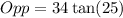
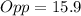 to the nearest tenth.
to the nearest tenth.
ii) We use the cosine ratio to find the hypotenuse;
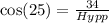
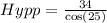
![Hypp=37.5/tex] units to the nearest tenth</p><p></p><p>QUESTION 4</p><p></p><p>i) We use the tangent ratio to find the opposite side length.</p><p></p><p>[tex]\tan(48\degree)=(Opp)/(17)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ic9qmnj9uqg9vwi296ntjf3w3kijqx70ty.png)
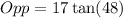
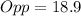 units to the nearest tenth
units to the nearest tenth
ii) We use the cosine ratio to find the hypotenuse;

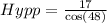
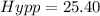 units to the nearest tenth.
units to the nearest tenth.
QUESTION 5
We use the sine ratio to find;

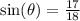
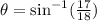
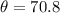
QUESTION 6
We use the tangent ratio to find the value of