Answer:

Explanation:
Given to equations to us are ,

And we need to find the solution using graphical method.
So , after plotting the graph of both equations the point where both lines intersect will be the solution of the graph.
And , for plotting we need at least two points .
For equation (1) :-

When x = (-4) .

When x = (-3)
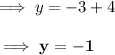

For equation 2 :-
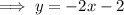
When x = (-1) .
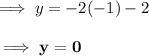
When x = (0)
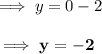

Now , let's plot their graphs. Graph is in attachment. Hence on plotting the graph we see that both the lines Intersect on (-2,2) . Hence x = -2 and y = 2 is the solution of the given linear equation.
Hence (-2,2) is the solution of the given pair of linear equations in two variables.