In slope-intercept form, the equation is

To find the equation of the linear function represented by the table in slope-intercept form
 , you need to determine the slope (\(m\)) and the y-intercept
, you need to determine the slope (\(m\)) and the y-intercept
 .
.
Let's use two points from the table to find the slope (\(m\)):
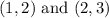
![\[ m = \frac{\text{Change in } y}{\text{Change in } x} \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xl1yvr9yv6du63s9rtl727yff25naneupq.png)
![\[ m = (3 - 2)/(2 - 1) = 1 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/omovm2wv66575exvek91h2wuecfqr8bh45.png)
Now that we have the slope (\(m = 1\)), we can use one of the points (let's use
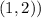 to find the y-intercept (\(b\)):
to find the y-intercept (\(b\)):
![\[ y = mx + b \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/v1ha8s4rr58lvfnhjdrsn9eztarecq28km.png)
![\[ 2 = 1 \cdot 1 + b \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ccx6v46o2u5j2k554g3jfzawhua48lqgdd.png)
![\[ b = 1 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/btws3k0dsdx5dzlg8gr7pyvg7sr59ikadq.png)
So, the equation of the linear function is:
![\[ y = x + 1 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/beomdipxwsr32ukg0lo8ze56nomi3qlh6x.png)