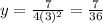Answer: option c
Explanation:
Based on the information given, you can write the following expression:

Where k is the the constant of variation
If y=7/4 when x=1, then you can substitute these values into the expression and solve for k:
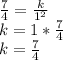
Substitute k into the expression. Then the equation is:
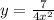
Substitute x=3 into the equation. Then, y is: