Answer with explanation:
If theta is replaced by , A,then the given statement will become
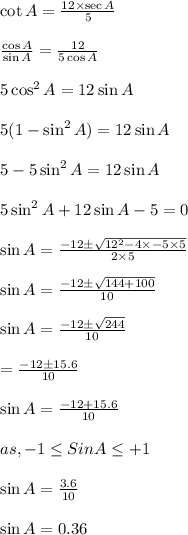
Which will be positive in second Quadrant.So,it is a true statement.
→If the statement is ,

And , A lies in second Quadrant,
Only ,Sine and Cosecant, Function are Positive in Second Quadrant.So,the statement, will be incorrect.