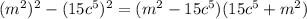Question

Replace ∗ with a monomial so that the result is an identity:

1. (2a+*)(2a-*)=4a^2-b^2
2. (5x+*)(5x-*)=25x^2-0.16y^4
3. (*-b^4)(b^4+*)=121a^10-b^8
4. (*-3x)(*+3x)=16y^2-9x^2
5. 100m^4-4n^6=(10m^2-*)(*+10m^2)
6. m^4–225c^10 = (m^2 − *)(* +m^2)

Answer 1

QUESTION 1

Taking the right hand side we have;

`4a^2-b^2`

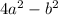
We can rewrite this as;

`(2a)^2-b^2`

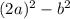
We apply difference of two squares.

`p^2-q^2=(p+q)(p-q)`

`(2a-b)(2a+b)`

`\therefore (2a-b)(2a+b)=4a^2-b^2`

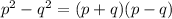
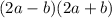
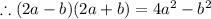
QUESTION 2

Taking the right hand side we have;

`25x^2-0.16y^4`

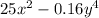
We can rewrite this as;

`(5x)^2-(0.4y^2)^2`

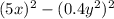
We apply difference of two squares.

`p^2-q^2=(p+q)(p-q)`

`(5x-0.4y^2)(5x+0.4y^2)`

`\therefore (5x-0.4y^2)(5x+0.5y^2)=25x^2-0.16y^4`

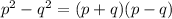
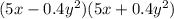
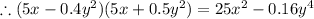
QUESTION 3

Taking the right hand side of the given equation, we have;

`121a^(10)-b^8`

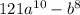
We rewrite this as;

`(11a^(5))^2-(b^4)^2`

`\therefore (11a^(5))^2-(b^4)^2=(11a^5-b^4)(11a^5+b^4)`

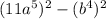
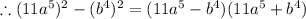
QUESTION 4

From the RHS;

`16y^2-9x^2`

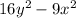
This implies that;

`(4y)^2-(3x)^2`

`(4y)^2-(3x)^2=(4y-3x)(4y+3x)`

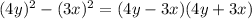
QUESTION 5

From the left hand side, we have

`100m^4-4n^6`

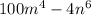
This implies that;

`(10m^2)^2-(2n^3)^2`

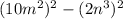
Using difference of two squares, we have;

`(10m^2)^2-(2n^3)^2=(10m^2-2n^3)(2n^3+10m^2)`

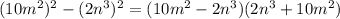
QUESTION 6

From the LHS;

`m^4-225m^(10)`

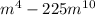
We rewrite to obtain;

`(m^2)^2-(15c^5)^2`

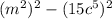
Using difference of two squares, we obtain;

`(m^2)^2-(15c^5)^2=(m^2-15c^5)(15c^5+m^2)`