Question

What is the sum of the first 21 terms of this arithmetic series?
-5+(-3)+(-1)+1+...

Answer 1

The sum of the first 21 terms of this arithmetic series is 315.

Explanation:

The given arithmetic series is

-5+(-3)+(-1)+1+...

Here first term is -5 and the common difference is

`d=-3-(-5)=2`

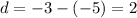
The sum of n terms of an AP is

`S_n=(n)/(2)[2a+(n-1)d]`

We need to find the sum of the first 21 terms of this arithmetic series.

Substitute n=21, a=-5 and d=2 in the above formula, to find the sum of the first 21 terms of this arithmetic series.

`S_(21)=(21)/(2)[2(-5)+(21-1)(2)]`

`S_(21)=(21)/(2)[-10+40]`

`S_(21)=(21)/(2)(30)`

`S_(21)=315`

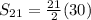
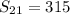
Therefore the sum of the first 21 terms of this arithmetic series is 315.

Answer 2

`S_(21)=315`

Explanation:

The given arithmetic series is

-5+(-3)+(-1)+1+...

The first term of this series is

`a_1=-5`

The common difference is

`d=-3--5`

`d=-3+5`

`d=2`

The sum of the first n-terms of an arithmetic sequence is

`S_n=(n)/(2)(2a+d(n-1))`

`S_(21)=(21)/(2)(2(-5)+2(21-1))`

`S_(21)=(21)/(2)(-10+2(20))`

`S_(21)=(21)/(2)(-10+40)`

`S_(21)=(21)/(2)(30)`

`S_(21)=(21)(15)`

`S_(21)=315`