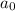Question

Given the general form of a polynomial function:


`P(x) = a_(n) x^(n) + a_(n-1) x^(n-1) + a_(n-2) x^(n-2) + . . . + a_(1) x^(1) + a_(0)`

The leading coefficient is ______.
The degree of the polynomial is ______.
The constant term of the polynomial is ______.

Answer 1

The leading coefficient is "a"

The leading degree of the polynomial is "n"

The constant term of the polynomial appears to be "a" again.

Explanation:

Answer 2

For this case we have given a polynomial of the form:

`P (x) = a_(n) x ^ {n} + a_ {n-1} x ^ {n-1} + a_ {n-2} x ^ {n-2} +. . . + a_ {1} x ^ {1} + a_ {0} x ^ 0`

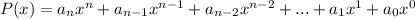
So:

x: It is the variable

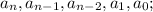`a_ {n}, a_ {n-1}, a_ {n-2}, a_ {1}, a_ {0};` They are the coefficients. Where
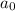`a_ {0}` is called a constant coefficient (or indendent term), and
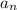`a_ {n}`is the main coefficient.

n, n-1, n-2,1,0: They are the exponents. where the largest represents the degree of the polynomial.

Answer:

The leading coefficient is
`a_ {n}`

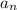
The degree of the polynomial is n

The constant term of the polynomial is
`a_ {0}`