Simplify and leave in radical form \sqrt[8]{x^2y^6}

Question

asked Feb 25, 2020 84.1k views

2 Answers

IEnumerator · Answer 1 · 2020-02-29T11:41:33+0000

For this case, we must simplify the following expression:

$\sqrt [8] {x ^ 2y ^ 6}$

By properties of powers and roots we have to:

$\sqrt [n] {a ^ m}$

It can be written equivalently as:

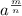
$a ^ {\frac {m} {n}}$

Then, the previous expression can be written as:

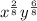
$x ^ {\frac {2} {8}} y ^ {\frac {6} {8}}$

Simplifying we have:

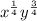
$x ^ {\frac {1} {4}} y ^ {\frac {3} {4}}$

Returning to the radical form we have:

$\sqrt [4] {xy ^ 3}$

Answer:

$\sqrt [4] {xy ^ 3}$