The inverse of the function f(x) =
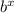 is the logarithmic function with base b, denoted as
is the logarithmic function with base b, denoted as
 (x) = log_b(x).
(x) = log_b(x).
The inverse of the function f(x) =
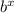 is the logarithmic function with base b, denoted as
is the logarithmic function with base b, denoted as
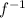 (x) = log_b(x). This means that for any value y,
(x) = log_b(x). This means that for any value y,
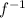 (y) is the value x such that f(x) = y. In other words, if f(x) =
(y) is the value x such that f(x) = y. In other words, if f(x) =
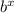 , then
, then
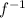 (y) = x when
(y) = x when
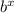 = y.
= y.
To see why this is true, consider the following equation:
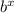 = y
= y
Taking the logarithm of both sides with base b, we get:
log_b(
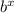 ) = log_b(y)
) = log_b(y)
Since log_b(
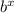 ) = x, we have:
) = x, we have:
x = log_b(y)
Therefore,
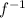 (y) = log_b(y).
(y) = log_b(y).