Question

A bird takes off at an angle of 30° to the ground with a velocity of 6 m/s. Which expression shows the bird’s height after 2 seconds?

Answer 1

A vector at an angle of 30° can be thought as the sum of a horizontal and a vertical vector, which we will call
`v_h,v_v`.

In particular, you have

`v = v_(h)+v_(v)`

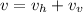
and moreover, we have

`v_(h) = v\cos(\alpha),\quad v_(v)=v\sin(\alpha)`

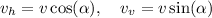
So, if we are only interested in the vertical component of the bird's flight, we have to consider a velocity of

`6\sin(30) = 6\cdot 0.5 = 3`

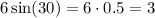
This means that the bird rises with a constant speed of 3m/s, and thus his equation is

`h = 3t`

where
`h` is the height in meters and
`t` is the time in seconds