Question

A pizza restaurant allow you to choose any 2 of 8 toppings. How many different ways are there to choose the toppings

Answer 1

answer = 8 * 7 / 2 = 28.

Explanation:

Answer 2

Answer with Step-by-step explanation:

Number of ways of choosing r items out of n are given by:

`(n!)/(r!(n-r)!)`

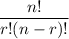
Here, we have to choose any 2 toppings out of 8

i.e. r=2 and n=8

So, number of ways are:

`(8!)/(2!(8-2)!)`

=
`(8!)/(2!6!)`

=
`(8* 7* 6!)/(2!6!)`

=
`(8* 7)/(2)`

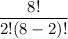
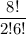
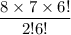
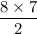
= 4×7

= 28

Hence, Number of ways to choose the toppings are:

28