Question

Which exponential function does not have an x-intercept? A. f(x) = 5x – 5 – 1 B. f(x) = 5x – 5 – 5 C. f(x) = -5x – 5 + 5 D. f(x) = -5x – 5 – 1

Answer 1

The correct option is (D)
`f(x)=-5^(x-5)-1`.

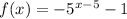Explanation:

Consider the option A.
`f(x)=5^(x-5)-1`

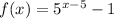
To find whether the exponential function has x intercepts, substitute
`f(x) = 0 \, \text {in} f(x)=5^(x-5)-1`.

`0=5^(x-5)-1`

`1=5^(x-5)`

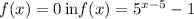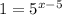
The above equality holds only for x = 5.

Now, consider the option B.
`f(x)=5^(x-5)-5`

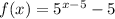
Similarly, substitute
`f(x) = 0 \, \text{in} f(x)=5^(x-5)-5`

`0=5^(x-5)-5`

`5=5^(x-5)`

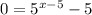
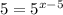
The above equality holds only for x = 6.

Consider the option C.
`f(x)=-5^(x-5)+5`

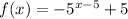
Substitute
`f(x) = 0 \, \text{in} f(x)=-5^(x-5)+5`

`0=-5^(x-5)+5`

`-5=-5^(x-5)`

`5=5^(x-5)`

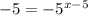
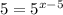
The above equality holds only for x = 6.

Now, consider the option D.
`f(x)=-5^(x-5)-1`

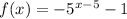
Substitute
`f(x) = 0 \, \text{in} f(x)=-5^(x-5)-1`

`0=-5^(x-5)-1`

`1=-5^(x-5)`

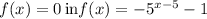
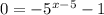
This equality never holds for any real number.

We can draw the graph for the provided options with the help of graphing utility.

We can verify our result with the help of figure 1.

From the figure 1, it is clear that the graph of
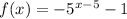`f(x)=-5^(x-5)-1` does not have an x intercept.

Hence, the correct option is (D)
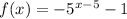`f(x)=-5^(x-5)-1`.

Answer 2

Option D does not have an x-intercept. Please se attached graph

Explanation:

To solve this equation easily, we graph each equation in a graphing calculator and see which of them doesn't intercept the x-axis.

The correct answer is option

D

f(x) = - 5^(x-5) - 1