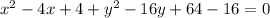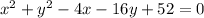Question

Write the equation of the translated graph in general form. x^2+y^2=16 for t (2,8)

(Picture provided below)

Answer 1

The general form of the translated circle is
`x^2+y^2-4x-16y+52=0`

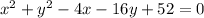
Explanation:

The equation of the given circle is:

`x^2+y^2=16`

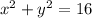
This is a circle that is centered at the origin;

This circle has been translated so that it is now centered at (2,8).

The translated will now have equation:

`(x-2)^2+(y-8)^2=16`

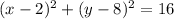
Expand:

`x^2-4x+4+y^2-16y+64-16=0`

`x^2+y^2-4x-16y+52=0`