Answer:
The sample size in this problem is students is 500.
The population proportion is estimated as 0.87.
The margin of error for this sample survey is 2.9.
Explanation:
It is given that a recent poll of 500 employees from a company of 1,300 employees was conducted.
It means the sample size in this problem is students is 500.
Of those polled, 435 feel that the minimum wage should be raised.
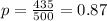
The population proportion is estimated as 0.87.
The formula for margin of error is
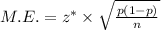
The desired confidence level of 95%, and a corresponding z*-score of 1.96. So, the margin of error for this sample survey is
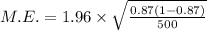
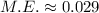
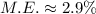
Therefore the margin of error for this sample survey is 2.9.