Answer:
Volume of snowman is 48π ft³
Explanation:
Since volume of a sphere =
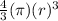
To find the volume of snowman we will find the volume of all spheres separately and add them.
Volume of sphere with radius 3 ft =
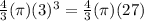 ft³
ft³
Volume of sphere with radius 2 ft =
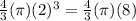
Volume of sphere with radius 1 ft =
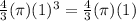
Total volume of the snowman =
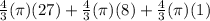
=
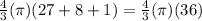
= 48π ft³
Therefore, total volume of the snowman = 48π ft³