Question

What is true about the solution above.

Answer 1

`x = \pm √(3)`

and they are actual solutions.

Step-by-step explanation

The given equation is:

`\frac{ {x}^(2) }{2x - 6} = (9)/(6x - 18)`

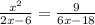
Cross multiply

`{x}^(2) (6x - 18) = 9(2x -6 )`

This implies;

`{x}^(2) (6x - 18) - 9(2x - 6) = 0`

`3{x}^(2) (2x - 6) - 9(2x - 6) = 0`

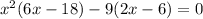
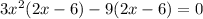
Factor

`(3 {x}^(2) - 9)(2x - 6) = 0`

`3 {x}^(2) - 9 = 0 \: or \: 2x - 6= 0`

`3 {x}^(2) = 9 \: or \: 2x = 6`

`{x}^(2) = 3\: or \: x = 3`

`{x} = \pm √(3) \: or \: x = 3`

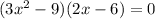
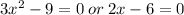
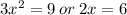
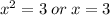
The domain of the given equation is

`x \\e3`

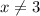
Therefore the actual solutions are

`x = \pm √(3)`

NB: x=3 is not in the domain of the given equation. It cannot be an extraneous solution.